Maßzahlen für die Lage

Unter dem Begriff „univariate Statistik“ versteht man die isolierte Betrachtung einzelner Merkmale bzw. Variablen von Untersuchungseinheiten (= Personen). Man macht nur Aussagen über ein einziges Merkmal (z.B. Alter). Bedeutsame Informationen liefern dabei Lagemaße und Streumaße.

Beispiel für eine Verteilung
Im Folgenden finden Sie ein Beispiel für eine eindimensionale Verteilung.
Erhoben wurde hierbei das Merkmal Alter.

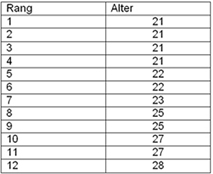
Die ursprüngliche Zuordnung einer Merkmalsausprägung zu einer Person nennt man Urliste:



Ordnet man die Urliste nach Stärke der Merkmalsausprägung ergibt sich die sortierte Liste daraus:

Diese kann man zur Häufigkeitsverteilung zusammenfassen:

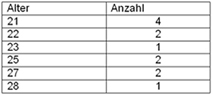
Es gilt: Die Summe der Häufigkeiten (Anzahl) ergibt die Gesamtanzahl der Teilnehmer N = (4+2+1+2+2+1) = 12

Extremwert / Modalwert

EXTREMWERTE

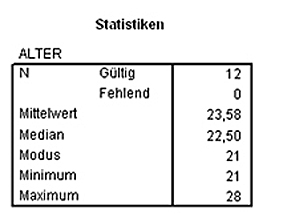
Unter Minimum versteht man den kleinsten Wert, der in einer Verteilung vorkommt. Das entspricht dem ersten Wert in der sortierten Liste. Im Beispiel liegt das Minimum für die Merkmalsausprägung Alter bei 21 Jahren.
Minimum (Alter) = 21

Analog dazu versteht man unter Maximum den größten Wert, der in einer Verteilung vorkommt. Das entspricht dem letzten Wert der sortierten Liste. Im Beispiel liegt das Maximum für die Merkmalsausprägung Alter bei 28 Jahren.
Maximum (Alter) = 28

MODALWERT

Der Modalwert ist derjenige Wert mit der größten Dichte, d.h. der häufigste Wert einer Häufigkeitsverteilung oder der Wert, mit der größten Wahrscheinlichkeit. Da eine Verteilung mehrgipflig sein kann, können einer Verteilung auch mehrere Modi zugeordnet sein. Der Modalwert ist am einfachsten aus der Häufigkeitstabelle abzulesen (siehe Grafik unten).

Graphische Darstellung einer Häufigkeitstabelle: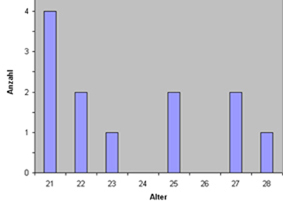

Im Beispiel liegt der Modalwert bei 21, diese Merkmalsausprägung kommt am häufigsten vor (4 mal).
Der Modalwert kann bei Daten ab Nominalskalenniveau bestimmt werden.

Median

Der Median wird auf Basis der „sortierten Liste“ bestimmt. Er bezeichnet allgemein eine Grenze zwischen zwei Hälften. In der Statistik halbiert der Median eine Stichprobe oder allgemein eine Wahrscheinlichkeitsverteilung.

Bei einer Stichprobe ist der Median definiert als jeder Beobachtungswert, bei dem die Werte jeweils mindestens der Hälfte der Beobachtungen kleiner oder gleich und die Werte mindestens der Hälfte größer oder gleich diesem Wert sind

Anders ausgedrückt:
Mindestens die Hälfte aller Werte ist kleiner gleich (<=) dem Median
Mindestens die Hälfte aller Werte ist größer gleich (>=) dem Median

Sortiert man die Beobachtungswerte der Größe nach („sortierte Liste“), so ist der Median bei einer ungeraden Anzahl von Beobachtungen der in der Mitte dieser Folge liegende Beobachtungswert.
Bei einer geraden Anzahl von Beobachtungen gibt es nicht ein mittleres Element, sondern zwei. Bei intervallskalierten Messgrößen verwendet man im Falle einer geraden Anzahl Beobachtungen meist das arithmetische Mittel der beiden mittleren Beobachtungswerte.

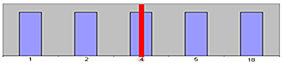
a) ungerade Anzahl
Messwerte 5, 2, 4, 18, 1 --> sortierte Liste: 1, 2, 4, 5, 18
Der Median ist der Wert an der mittleren Stelle der sortierten Liste, diese errechnet sich folgendermaßen:
(Anzahl der Messwerte +1) / 2, d.h. (5+1) / 2 = 3 --> der Median ist der dritte Messwert, also 4.

b) gerade Anzahl
Messwerte 4, 1, 3, 2, 37, 1 --> sortierte Liste: 1, 1, 2, 3, 4, 37
Der Median liegt  bei der Hälfte der Summe der beiden mittleren Zahlen der sortierten Liste und errechnet sich folgendermaßen:
(Anzahl Teilnehmer) / 2 + [(Anzahl Teilnehmer / 2) +1]

für obiges Beispiel bedeutet das:
[6 / 2]= 3 (--> der dritte Wert ist 2)
[6 / 2] + 1 = 4 (--> der vierte Wert ist 3)
Der Median liegt also zwischen dem dritten und vierten Wert.

Das Mittel über diese beiden mittleren Werte ist [(2+3) / 2], der Median liegt also bei 2,5.
Der Median kann bei Daten ab Ordinalskalenniveau bestimmt werden.

Arithmetisches Mittel

Der Mittelwert wird berechnet, indem die Summe der Einzelwerte des Datenbündels durch die Zahl der Elemente dividiert wird.
Aufgabe des arithmetischen Mittels ist es, Aufschluss über den Durchschnittswert vorliegender Werte zu geben.

Es wird folgendermaßen berechnet: 

für das Beispiel ergibt sich:

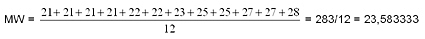
Das arithmetische Mittel beinhaltet Informationen über die Lage eines Datenbündels. Es erfordert mindestens Intervallskalenniveau.
 
Das arithmetische Mittel (MW) wird auch als Durchschnitt oder Schwerpunkt bezeichnet. Die Eigenschaft als Schwerpunkt kann anhand eines graphischen Beispiels verdeutlicht werden. Eine Balkenwaage, bei der die Gewichte am Balken hängen hat beim arithmetischen Mittel Ihren Schwerpunkt.

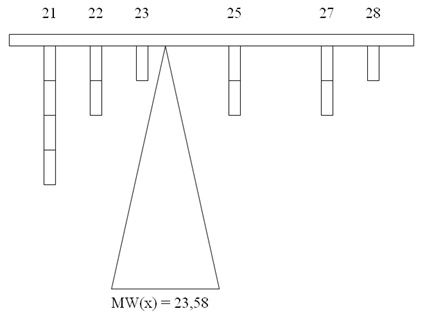
Interpretation
Das arithmetische Mittel kann als Durchschnittswert eines Datenbündels bzw. einer Verteilung interpretiert werden.
Für obiges Beispiel bedeutet das: das Durchschnittsalter der Teilnehmer beträgt knapp 23,58 Jahre.

Alternative Interpretation
Bei einer repräsentativen Stichprobe würde man das Alter einer beliebigen Person der Grundgesamtheit auf den Mittelwert schätzen (in diesem Fall würde man den Teilnehmer auf 23,5833 Jahre tippen). Mit diesem Schätzwert würde man, wenn alle Teilnehmer bezüglich ihres Alters geschätzt werden sollten, und die Fehler über alle diese Schätzungen aufaddiert werden würden, die (in der Summe) wenigsten Fehler machen.

Median vs. arithmetisches Mittel: Vor- und Nachteile

Welche Maßzahl ist wann geeignet?

Der Median ist robust (d.h. nicht anfällig) gegenüber extremen Ausreißern, das arithmetische Mittel nicht.

Beispiel: Es liegen 2 Einkommenslisten vor, die sich nur in einem Wert unterscheiden
Liste A: 100, 100, 100, 100, 100, 1300
Liste B: 100, 100, 100, 100, 100, 300

Der Median liegt sowohl bei Liste A als auch bei Liste B bei 100

Das arithmetische Mittel für Liste A liegt bei 300, für Liste B bei 133,33
--> Der Großverdiener in Liste A verändert das arithmetische Mittel stark, nicht aber den Median

Das arithmetische Mittel ist robust bei internen Werteverschiebungen, nicht aber der Median
Beispiel: 2 Vermögenslisten, bei denen einer später allen anderen etwas wegnimmt

Liste A: 200, 200, 200, 200, 200, 200
Liste B: 100, 100, 100, 100, 100, 700

--> Das arithmetische Mittel liegt sowohl für Liste A als auch für Liste B bei 200
Der Median liegt für Liste A bei 200, für Liste B bei 100

WICHTIG: Das arithmetische Mittel erfordert mindestens Intervallskalenniveau, der Median erfordert lediglich Ordinalskalenniveau!!!!

Alternativen zum arithmetischen Mittel

Um die Anfälligkeit des arithmetische Mittels gegen Extremausreißer abzuschwächen kann man auf zwei alternative Vorgehensweisen zurückgreifen:

Das getrimmte Mittel:
Hierbei wird ein vorher festzulegendes Quantum q (z.B. 10%) der kleinsten und größten Werte eliminiert. Anschließend wird das arithmetische Mittel über die verbleibenden Werte berechnet:

Datenbeispiel:  21, 21, 21, 21, 22, 22, 23, 25, 25, 27, 27, 28
Man berechnet nun, wie viele Werte wegfallen: Anzahl Teilnehmer * q

für obiges Beispiel: 12 * 0,1 = 1,2 --> Zahlen hinter dem Komma können vernachlässigt werden, d.h. auf beiden Seiten der Daten fällt je ein Wert weg

21, 21, 21, 21, 22, 22, 23, 25, 25, 27, 27, 28

--> der kleinste (21) und der größte (28) Wert fallen weg

dann gilt: Getrimmtes Mittel = (3*21 + 2*22 + 1*23 + 2*25 + 2*27) / 10 = 234/10 = 23,4

Das winsorisierte Mittel:
Hierbei wird ein vorher festzulegendes Quantum q (z.B. 10%) der kleinsten bzw. größten Werte durch weniger extreme Werte ersetzt. Die Ersatzwerte sind dabei jeweils die ersten, die nicht mehr wegfallen.

Datenbeispiel: 21, 21, 21, 21, 22, 22, 23, 25, 25, 27, 27, 28
Vorgehen: Berechnung wie viele Werte wegfallen: Anzahl Teilnehmer * q

für obiges Beispiel: 12 * 0,1 = 1,2 --> Zahlen hinter dem Komma können vernachlässigt werden, d.h. es wird auf beiden Seiten der Daten je ein Wert ersetzt.
21, 21, 21, 21, 22, 22, 23, 25, 25, 27, 27, 28

Der kleinste Wert (21) wird durch den ersten nicht mehr wegfallenden Wert (21) ersetzt.
Der größte Wert (28) wird durch den ersten nicht mehr wegfallenden Wert (27) ersetzt.

dann gilt: Winsorisiertes Mittel = (4*21 + 2*22 + 1*23 + 2*25 + 3*27) = 282/12= 23,5

Die Interpretation beider beschriebener Alternativen erfolgt analog zur Interpretation des arithmetischen Mittels.

Berechnung der Lagemaße mit SPSS

Besonders für große Datensätze wäre es sehr aufwendig die erläuterten Kennzahlen manuell zu berechnen. Es empfiehlt sich daher die Nutzung einer speziellen Statistik-Software. Eine weit verbreitete Statistik-Software ist SPSS. Im Folgenden wird nun kurz erklärt, wie Sie die beschriebenen Maße in SPSS berechnen können. Eine detaillierte Einführung in SPSS finden Sie in unserer Anleitung für SPSS.

Gehen Sie folgendermaßen vor:
Wählen Sie in SPSS das Menü „Analysieren“ --> „Deskriptive Statistiken“ --> „Häufigkeiten“.
Es öffnet sich ein neues Fenster. In diesem sehen Sie links alle vorhandenen Variablen aufgelistet. Wählen Sie nun diejenige Variable aus, für die Sie die Maße berechnen lassen möchten (hier: Alter). Markieren Sie dazu die entsprechende Variable und klicken Sie anschließend auf den Pfeil (rot markiert), der die Variable in das rechte Feld verschiebt.

-->

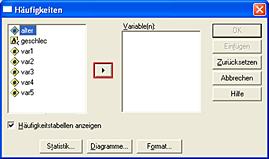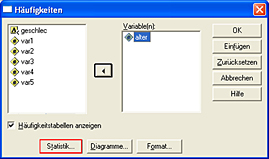Klicken Sie jetzt auf den "Statistik"-Button. Es öffnet sich ein neues Fenster, in dem Sie die gewünschten Maße auswählen können.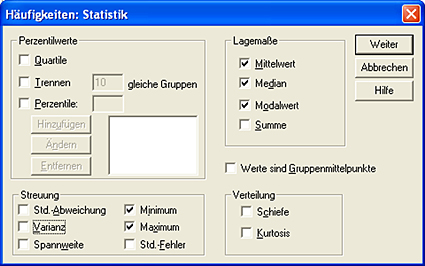

Klicken Sie nun auf den "Weiter"-Button. Es erfolgt die Berechnung der gewünschten Kennzahlen, die unsere manuell berechneten Ergebnisse bestätigen: