Zusammenhangsmaß für zwei intervallskalierte Variablen

Der Korrelationskoeffizient r ist das bekannteste statistische Zusammenhangsmaß. Er wird als statistisches Maß für den linearen Zusammenhang zwischen zwei mindestens intervallskalierten (d.h. metrischen) Variablen verwendet.

Der Korrelationskoeffizient kann dabei Werte zwischen minimal -1 und maximal +1 annehmen, wobei -1 einen perfekten negativen ("je größer X, desto kleiner Y") und +1 einen perfekten positiven ("je größer X, desto größer Y") Zusammenhang bezeichnet
Wenn der Korrelationskoeffizient den Wert 0 aufweist, hängen die beiden Merkmale überhaupt nicht linear zusammen. Allerdings können diese ungeachtet dessen in nicht-linearer Weise (z.B. U-förmig) zusammenhängen.

Es gilt:
Die Korrelation zwischen X und Y entspricht der Korrelation zwischen Y und X
Die Korrelation zwischen X und X ist immer 1
Die Korrelation zwischen Y und Y ist immer 1

Eine Korrelation größer +1 oder kleiner -1 kann niemals auftreten.

Berechnung des Korrelationskoeffizient

Um den Korrelationskoeffizienten berechnen zu können muss man vorher Mittelwerte und Standardabweichungen von X und von Y, sowie die Kovarianz zwischen X und Y berechnen.

Die Formel für den Korrelationskoeffizient lautet: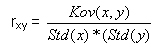

Ein Datenbeispiel: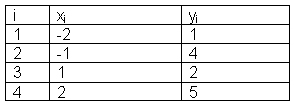

Zuerst werden nun die Mittelwerte von X und Y berechnet:

Berechnung des Mittelwerts von X :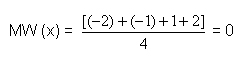

Berechnung des Mittelwerts von y: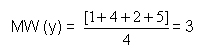

Es folgt die Berechnung der Standardabweichungen von X und Y.
Berechnung der Standardabweichung von X: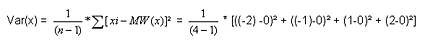

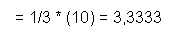
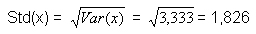
Berechnung der Standardabweichung von Y: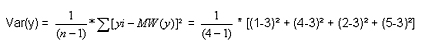

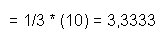
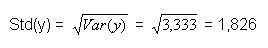
Nun folgt die Berechnung der Kovarianz zwischen X und Y. Die Kovarianz wird mit folgender Formel berechnet: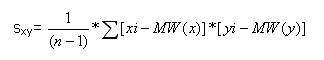

Es ergibt sich:

Hier: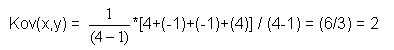


Berechnung des Korrelationskoeffizienten: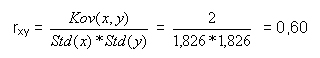

Berechnung des Korrelationskoeffizient mit Hilfe von SPSS

Wählen Sie im Menü „Analysieren“ --> „Korrelation“ --> „bivariat“

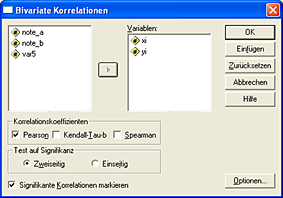
Wählen Sie die beiden Variablen aus, für die der Korrelationskoeffizient berechnet werden soll. Wählen Sie unter Korrelationskoeffizienten „Pearson“ aus.
Wenn Sie auf den „Optionen“-Button klicken können Sie sich zusätzlich die Mittelwerte und Kovarianzen anzeigen lassen.
Klicken Sie nun auf den „OK“-Button.
SPSS bestätigt unsere manuell berechneten Ergebnisse:

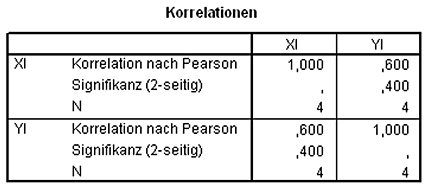
Interpretation des Korrelationskoeffizienten

Da bei der Interpretation des Korrelationskoeffizienten häufig Fehler gemacht werden, widmen wir uns diesem Themengebiet in aller Ausführlichkeit.

Das oberste Gebot bei der Interpretation des Korrelationskoeffizienten lautet: Es handelt sich lediglich um ein Maß für den Zusammenhang zweier Variablen

Kausale Aussagen (Ursache-Wirkungs-Aussagen) sind nicht zulässig!

Beispiel zur Verdeutlichung:
Empirische Untersuchungen haben gezeigt, dass ein Zusammenhang besteht zwischen der Anzahl von Feuerwehrautos am Brandort und der Höhe des Brandschadens.
Daraus ließe sich nun folgender (kausaler) Schluss ziehen: je mehr Feuerwehrautos bei einem Brand im Einsatz sind, desto höher der Schaden.
Das ist natürlich Unfug, verdeutlicht aber die Schwierigkeit der Interpretation.

Außerdem ist es möglich, dass die beiden Variablen lediglich über eine andere, dritte Variable zusammenhängen. Man spricht dann von einer so genannten Scheinkorrelation.

Dazu ein weiteres Beispiel:
Eine Analyse über die letzten 50 Jahre hat ergeben, dass die Besiedlung durch Störche im Norden Baden-Württembergs positiv mit der dortigen Geburtenzahl korreliert. Das bedeutet natürlich noch lange keinen kausalen Zusammenhang - weder bringen Störche Kinder noch umgekehrt. Trotzdem ist ein statistischer Zusammenhang gegeben. Dieser leitet sich aber aus einem dritten Faktor ab, wie z.B. der Verstädterung, die sowohl Nistplätze vernichtet als auch Kleinfamilien fördert.

Für die Interpretation des Korrelationskoeffizienten ist also stets Vorsicht geboten!

Bei Zusammenhangsmaßen für sozialwissenschaftliche Daten gelten folgende Faustregeln:

	r	=1	--> perfekter Zusammenhang
0,7 <	r	< 0,99	--> sehr starker Zusammenhang
0,5 <	r	< 0,69	--> starker Zusammenhang
0,3 <	r	< 0,59	--> mittelstarker Zusammenhang
0,2 <	r	< 0,29	--> schwacher Zusammenhang
	r	<=0,19	--> kein Zusammenhang

Das Quadrat des Korrelationskoeffizienten r² nennt man Bestimmtheitsmaß (= Determinationskoeffizient). Es gibt in erster Näherung an, wie viel % der Varianz durch die untersuchte Beziehung erklärt werden. Beispiel: Bei r = 0,3 bzw. 0,8 werden 9% bzw. 64% der gesamten auftretenden Varianz im Hinblick auf einen statistischen Zusammenhang erklärt.