Zusammenhangsmaß für zwei ordinalskalierte Variablen

Rangkorrelationskoeffizient Spearmans rho

Dieses Maß ist ab ordinalem Skalenniveau gültig und betrachtet die Rangplatzdifferenz (di) von zwei verschiedenen Beurteilungen bei zwei ordinalskalierten Merkmalen

Beispiel:
Die Teilnehmerinnen an einem Eiskunstlauf-Wettbewerb werden von zwei Punktrichtern (Punktrichter A und Punktrichter B) bewertet. Nun stellt sich die Frage, ob die Läuferinnen die von Punktrichter A gut bewertet wurden (x-Wert) tendenziell auch von Punktrichter B gut bewertet wurden (y-Wert).

Es werden nun zunächst alle x-Werte und alle y-Werte in Ränge umgewandelt. Demzufolge besitzt jede Läuferin einen Rang x und einen Rang y. Die Differenz Rang x – Rang y ergibt dann die Rangdifferenz di, welche später aufaddiert in die Formel eingesetzt wird.

Für die Berechnung von Spearman?s rho mit der mathematischen Formel ist es notwendig, nicht die ordinalen Ausgangswerte, sondern die Ränge zu verwenden. Diese werden dann quasi wie echte metrische Zahlen behandelt.

Die Formel für Spearmans rho lautet:

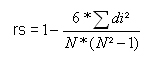
Ein Beispiel zur Verdeutlichung: Aufgelistet finden Sie die Noten von zwei Punktrichtern beim Eiskunstlauf für 4 Läuferinnen.

Zuerst werden aus den Noten von Punktrichter A Ränge gebildet. Diejenige Läuferin, die die beste Note bekommen hat erhält Rang 1, die mit der zweitbesten Note Rang zwei usw. Analog werden anschließend die Ränge für Punktrichter B gebildet.

Spezialfall: Wenn zwei Läuferinnen von einem Punktrichter dieselbe Note erhalten, wird der Durchschnittsrang berechnet (z.B. beide Läuferinnen erhalten die Bestnote 5,6  zu vergeben wären die Ränge 1 und 2  beide erhalten dann Rang (1+2)/2 = 1,5).

Wichtig: Die Formel für Spearman?s rho ist nur gültig, wenn weniger als 20% der vergebenen Ränge dem oben beschriebenen Spezialfall entsprechen, d.h. weniger als 20% der vergebenen Ränge sind gleich.

Für das obige Beispiel entsteht folgende Rangtabelle:

Nun werden die Rangdifferenzen (A-B) berechnet:

Die Summe aus di² beträgt 6. N beträgt 4 (da hier 4 Läuferinnen bewertet wurden).
Die Berechnung von rs ergibt folgendes: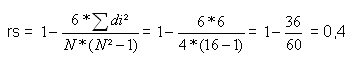

Berechnung von Spearmans rho mit Hilfe von SPSS

Wählen Sie im Menü „Analysieren“ --> „Korrelationen“ --> „Bivariat“

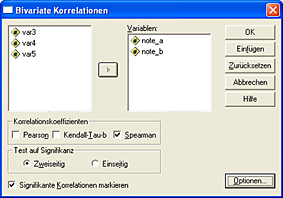
Wählen Sie die beiden Variablen aus, für die das Zusammenhangsmaß berechnet werden soll. Markieren Sie unter Korrelationskoeffizienten „Spearman“. Klicken Sie nun auf den "OK"-Button, SPSS zeigt Ihnen die Ergebnisse folgendermaßen an:

Anhand der Ergebnisausgabe für Spearmans-Rho besprechen wir die Ergebnisdarstellung von Zusammenhangsmaßen ab Ordinalskalenniveau in SPSS allgemein:
Rein formal erfolgt die Ergebnisausgabe in SPSS in Kreuztabellen:

Es gilt: Auf der Diagonalen befinden sich die Zusammenhänge eines Merkmals mit sich selbst. Das bedeutet konkret: In Feld 1 ist der Zusammenhang von Merkmal A mit Merkmal A abgebildet, in Feld 4 der Zusammenhang von Merkmal B mit Merkmal B. Diese Zusammenhänge sind per Definition immer 1 und daher für die Auswertung uninteressant.

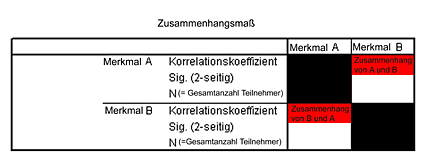
In Feld 2 befindet sich der Zusammenhang von Merkmal A mit Merkmal B, in Feld 3 der Zusammenhang von Merkmal B mit Merkmal A. Da sich diese beiden per Definition entsprechen, reicht zur Ergebnisanalyse die Betrachtung eines der beiden Felder (2 oder 3) aus. In den beiden rot markierten Feldern stehen also identische
Zahlen. Zur Interpretation der Ergebnisse reicht folglich ein Blick auf Feld 3 (alternativ geht natürlich auch Feld 2):

Den Wert für Spearmans Rho finden Sie neben „Korrelationskoeffizient“. Darunter finden Sie Werte für die Signifikanz. Auf dieses Themengebiet gehen wir in diesem Dokument nicht näher ein. Bei Interesse empfehlen wir Ihnen eines der gängigen Statistik-Werke.
Unterhalb der Signifikanz finden Sie die Gesamtanzahl der Datensätze (= Teilnehmer), die in die Analyse eingegangen ist.

Nach dieser Einleitung zum Grundverständnis der Ergebnisausgabe bei SPSS wenden wir uns wieder unserem konkreten Datenbeispiel zu.
Für obigen Datensatz bestätigt sich unser manuell berechneter Wert von 0,4 für Spearmans Rho:

Interpretation
Ein Spearmans Rho – Wert von 0,4 besagt, dass eine mittelstarke positive Beziehung zwischen der Bewertung durch Punktrichter A und der Bewertung durch Punktrichter B besteht. D.h. eine Läuferin, die von Punktrichter A gut bewertet wurde, wird tendenziell auch von Punktrichter B gut bewertet.
Einschränkung: Unsere Stichprobe mit 4 Läuferinnen ist zu klein, um allgemein gültige Rückschlüsse zu ziehen.

Berechnung von Tau-b

Eine etwas andere Vorgehensweise wird mit der Berechnung von Tau b verfolgt. Die Logik von Tau b beruht darauf, jede einzelne Untersuchungseinheit mit jeder anderen Untersuchungseinheit zu vergleichen. Man könnte sagen, diese Vergleiche laufen paarweise ab, daher ist im Folgenden oft von „Paaren“ die Rede.

Beim paarweisen Vergleich bei Ordinalskalenniveau werden jeweils zwei Objekte beziehungsweise Personen bei zwei Bewertungen gleichzeitig betrachtet. Ich kann also Läuferin 1 und Läuferin 2 als erstes Paar bilden. Jetzt haben beide Läuferinnen eine Note von Punktrichter A (x) und eine Note von Punktrichter B bekommen (y)
Es wird nun folgendermaßen vorgegangen:

Man führt die X-Betrachtung durch, d.h. es wird untersucht ob Läuferin 1 besser als Läuferin 2 von Punktrichter A bewertet wurde. Anschließend wird betrachtet ob  Läuferin 1 AUCH von Punktrichter B als Läuferin 2 bewertet wurde (sog. Y-Betrachtung).
--> Es werden also immer zwei Objekte (in diesem Fall Läuferinnen) mit zwei Bewertungen (Punktrichter A und Punktrichter B) betrachtet.
Von Konkordanz spricht man, wenn Läuferin 1 von beiden Punktrichtern besser (oder schlechter) als Läuferin 2 bewertet wurde.

Ein Wertepaar ist diskordant, wenn Läuferin 1 von einem der Punktrichter besser und von einem schlechter als Läuferin B Bewertet wurde.

Wenn Läuferin 1 von einem Punktrichter dieselbe Note bekommt wie Läuferin 2 spricht man von einem Tie.
Dabei gilt: Kommt dieselbe Note von Punktrichter A handelt es sich um ein Tie x, kommt dieselbe Note vom Punktrichter B um ein Tie y und bewerten beide Punktrichter beide Läuferinnen gleich spricht man von einem Tie xy.

--> Tau b betrachtet das Verhältnis zwischen konkordanten und diskordanten Paaren unter Berücksichtigung der Ties.

Zum besseren Verständnis ein paar Beispiele:

Konkordantes Paar:

Läuferin 1 wird von Punktrichter A (5,7 vs. 5,3) und von Punktrichter B (5,5 vs. 5,4) besser bewertet als Läuferin 2.

Konkordantes Paar:

Läuferin 1 wird von Punktrichter A (5,2 vs. 5,4) und von Punktrichter B (5,1 vs. 5,2) schlechter bewertet als Läuferin 2.

Diskordantes Paar:

Läuferin 1 wird von Punktrichter A schlechter als Läuferin 2 bewertet, von Punktrichter B wird sie aber besser als Läuferin 2 bewertet.

Diskordantes Paar:

Läuferin 1 wird von Punktrichter A besser als Läuferin 2 bewertet, von Punktrichter B wird sie aber schlechter als Läuferin 2 bewertet.

Tie x:

Die beiden Läuferinnen erhalten von Punktrichter A dieselbe Bewertung. Es kann kein Rang gebildet werden.

Tie y:

Die beiden Läuferinnen erhalten von Punktrichter B dieselbe Bewertung. Es kann kein Rang gebildet werden.

Tie xy:

Die beiden Läuferinnen erhalten von Punktrichter A und Punktrichter B dieselbe Bewertung. Es kann bei beiden Bewertungen kein Rang gebildet werden.

Für Tau b gilt:

• Tau b ist definiert als das Verhältnis des Übergewichts konkordanter oder diskordanter Paare zur Gesamtzahl aller möglichen Paare
• Tau b liegt immer zwischen -1 und +1. Ein Zahlenwert Null für Tau b besagt, dass die Anzahl der konkordanten und diskordanten Paare gleich groß ist, ein Zahlenwert +/- 1 sagt aus, dass es entweder nur konkordante oder nur diskordante Paare gibt.
• Tau b kann bei beliebig großen Tabellen angewendet werden, kann aber nur dann einen Wert von +/- 1 annehmen, wenn es sich um eine so genannte quadratische Tabelle (z.B. 3x3-Tabelle) handelt.
• Für 2*2 Tabellen ergibt der Koeffizient Tau b denselben Zahlenwert wie der Koeffizient Phi

Zur Verdeutlichung ein Daten-Beispiel:

Es gibt folgende Paare: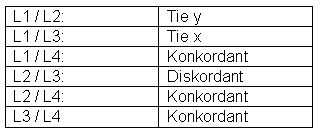

Tau b berechnet sich nun folgendermaßen: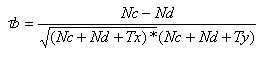 



Mit :
Nc: Anzahl konkordanter Paare
Nd: Anzahl diskordanter Paare
Tx: Ties in x
Ty: Ties in y

Für das Beispiel ergibt sich: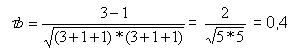

Berechnung von Tau-b mit Hilfe von SPSS

Wählen Sie im Menü „Analysieren“ --> „Korrelation“ --> bivariat. Es öffnet sich folgendes Fenster:

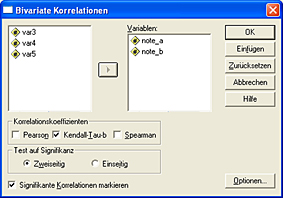
Wählen Sie die beiden Variablen aus, für die das Zusammenhangsmaß berechnet werden soll. Wählen Sie unter Korrelationskoeffizienten „Kendall-Tau-b“ aus, klicken Sie dann auf den „OK“-Button.
SPSS bestätigt unsere manuell berechneten Ergebnisse:

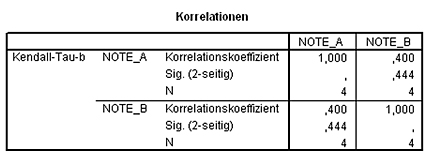
Interpretation
Es besteht ein mittelstark positiver Zusammenhang zwischen der Bewertung durch Punktrichter A und der Bewertung durch Punktrichter B. Es gibt ein mittelstarkes Übergewicht an Konkordanten Paaren. Das bedeutet, die Läuferin, die von Punktrichter A besser bewertet wird, wird tendenziell auch von Punktrichter B besser bewertet.
Auch hier gilt die Einschränkung, dass die Stichprobe zu klein ist, um allgemein gültige Rückschlüsse zu ziehen.